[程式設計]15. 3Sum

簡介

3Sum 是 LeetCode 的一道面試題，難度為「難」。

題目是這麼說的

給一個陣列，包含了 n 個整數 (有正數，也有負數)。

請在裏面找 3 個數，x，y 以及 z，滿足  x + y + z = 0。

此外還要求找出的 x, y, z 不可以重覆。

例如在底下的陣列中

[-4, -1, -1, 0, 1, 2]

你可以湊出 2 個 [-1, 0, 1] 以及 [-1, 0, 1]

但其實另一個 [-1, 0, 1] 是不必要的。

這個問題難在面試時，公司要求寫出「有效率」的程式碼。

但這題要如何有效率解出，是有難度的。

就直覺來說，我們會使用 3 層迴圈來搞定，程式碼如下所示：

上面程式碼是錯的，因為所回傳的資料有重覆的問題。但基本上來說，已經有初步的形態了。雖然程式碼是有錯的，但瞭解這部分，對於後續程式碼的瞭解，有很大的幫助，因此請確實搞懂它的運作狀況。

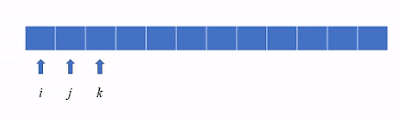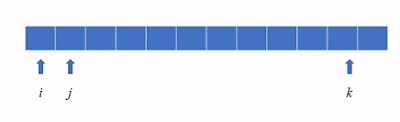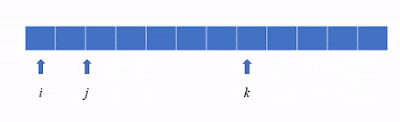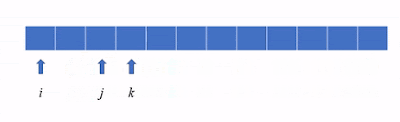
下圖是這支程式基本的執行狀況 (只展示部分)。一開始 i、j及 k 三個索引都指向開頭。

k 掃描完剩餘的格子後， j 會指向下一個元素，然後 k 再掃描剩餘的元素，依此類推。

這個解是 O(n^3) 的時間複雜度，通過不了面試公司「有效率」的要求。

解決重覆的問題

先來解決重覆的問題。要解決重覆，先要知道重覆是怎麼發生的。

由下圖可以看到，時間點 1 時，nums[i]，nums[j] 以及 nums[k] 會湊出 [-5, 2, 3]。
在時間點 2時，nums[i]，nums[j] 以及 nums[k] 「也」會湊出 [-5, 2, 3]，於是重覆發生！在這個情況中， i 索引值在「時間點1」以及「時間點2」都指到了同樣的值。

以程式碼的角度來看，就是 nums[i] 及 nums[i - 1] 的值若是一樣時，那表示 索引 i 讀到了「曾經出現的值了」。

3SUM 可能重覆的狀況之一

再來看另一種情況，由下圖來看。nums[i]、nums[j]以及nums[k]在兩個間點都會湊出 [-5, 2, 3] 這樣的結果，於是重覆發生！

這個情況是 j 索引值指到了重覆的值。

以程式碼的角度來看，就是 nums[j] 及 nums[j - 1] 的值若是一樣時，那表示 索引 j 讀到了「曾經出現的值了」。

3sum 可能重覆的狀況之二

同樣的，k 指到同樣的值，也是會發生重覆，例子大家可以自己想想囉。


所以情況很清楚了，只要 i 或 j 或 k 指到曾經出現過的值，那就會發生「重覆」。所以只要能避免這種狀況，就避開「產生重覆結果」的狀況了。

依照這種想法，我們改善了第一種寫法，得到了底下的程式碼。這支程式碼已經可以輸出「正確」的結果了，但還是個 O(N^3) 的解法，不能滿足效率的要求。

解說一下這支程式碼的幾個重點。

第 11 行是先把 nums 排序！這行很重要，底下偵測重覆的程式碼之所以可以運作，都是因為有先排序的原因。

事實上，「排序」可以說是「加速」的基礎。因為排序後，資料就會呈現一個規律的狀況 (例如資料由小到大排），而這個狀況，可以讓我們加以利用，找出許多可以加速的技巧。

關於這點，我們後面還會看到例子。

第 14 - 15 行是看看 i 索引值有沒有讀到曾經出現過的值，如果有，就略過這個值。

同樣的，第 18 - 19 行也是看看 j 索引值有沒有讀到曾經出現過的值，如果有，就略過這個值。

同理， 22- 23 行是看 k 索引值有沒有讀到曾出現過的值。

接著討論如何加速

我們可以再改善前一支程式，想法子讓它加速。

使用排序的特性

想法是這樣的，如果我們發現 nums[i] 的值已經「大於 0」了，那就沒必要再做下去。

因為 nums 是由小到大排序過了，所以 nums[i] 大於 0，表示 nums[j] 及 nums[k] 也都大於 0，大於 0 的值不可能相加後會滿足 nums[i] + nums[j] + nums[k] == 0。所以就可以停止了。

下圖展示了一個可能性。這個例子中 nums[i] == 1 > 0，所以 nums[i] + nums[j] + nums[k] 一定大於 0。

nums[i] > 0，那麼 nums[i] + nums[j]  + nums[k] 一定也 > 0

延伸前面的想法，我們也可以得到：

若 nums[i] + nums[j] > 0，那也可以停止程式的執行。理由相信你也推得出來。

再延伸，我們可以得到 nums[i] + nums[j] + nums[k] > 0，一樣可以停止執行。

因此可以得到底下的程式碼：


這支程式有加速了，但很遺憾，還是個 O(n^3) 的方法，最差情況，還是要花大量的時間。因此還是通不過 LeetCode 的要求。

底下使用另一個雙指標的方式來加速！

使用雙指標

這兒我們採用 2 points (雙指標，或稱雙索引值) 的作法。基本的運作方式如下圖所示。

當 i 索引值指到某個元素時， j 及 k 兩個索引值，一個由頭往後，一個由尾巴往前，開始掃描，直到 j 及 k  相遇為止。

這兒有個重要的特性要記得：因為資料已經排序過了，所以 j 所讀到的值，會「越來越大」。 k 所讀到的值，會「越來越小」。這個特性我們之後會用到。

所以現在固定 i。 然後 j 及 k 不斷的變化。這時 nums[i] + nums[j] + nums[k] 有三種可能性！

1. nums[i] + nums[j] + nums[k] == 0：這種情況太好了，我們找到一個解答，當然把解答存起來。
2. nums[i] + nums[j] + nums[k] > 0：這個時後 j 不用動。k 要動。為什麼？因為 j 所讀的資料是越來越大，再動 j 的話，結果只會變大，就不可能得到等於 0 的結果了。而 k 所讀的值會越來越小，所以動 k 的話，有機會找到 nums[i] + nums[j] + nums[k] == 0 的結果。
3. nums[i] + nums[j] + nums[k] < 0：這個情況和上一個情況相反。我們要動 j，不要動 k。相信你可以推得出來原因。

所以我們只要處理這三個 cases，就可以搞定了！程式碼如下：

程式碼中，19-40行是最重要的核心。也是雙索引值啟動的地方。
21 - 25 行還是在判斷 j 有沒有讀到曾經出現過的值，要是有的話，就跳掉這個值。

接著第 26 行是 case 1。記得處理完後，要把 j 的值加 1。

31 行是 case 2。

35 行是 case 3。

原理在前面的說明都談過了，程式碼也很簡單，所以我就跳過不說明了。

程式的複雜度

分析一下雙指標的寫法。

當固定 i 後， j 和 k 要掃描剩餘的資料。所以要花 n 的時間。

因為每固定一次 i ，就要花 n 的時間掃一次 nums。 所以整體的複雜度為 O(n^2)。

相較於前面的 O(n^3) 的解法，大量節省了時間，是可以通過 LeetCode 的要求的。

結尾

3Sum 看似是個簡單的題目，但因為效率的要求，所以要使用較複雜的邏輯來處理。

整個加速的流程的核心重點是「排序」。也因為排序過，所以有許多的加速機制可以用上。

因此日後要是遇到有需要效率的狀況，或者先排序一下，可能可以想出許多可以加速的技巧。